概要
利回りの変化に対する債券価格の変化は曲線状となるのに対して、 デュレーションは利回りの変化に対する債券価格を線形近似するも のであるため、デュレーションのみでは金利水準の変化による債券 価格の変化を完全には説明できません。金利水準の変化により債 券のデュレーション自体が変化してしまうため、金利水準が大きく 変化するほどデュレーションのみでは説明されない部分がより大き くなります。そこで、デュレーションを補完するために、コンベクシティ が用いられます。
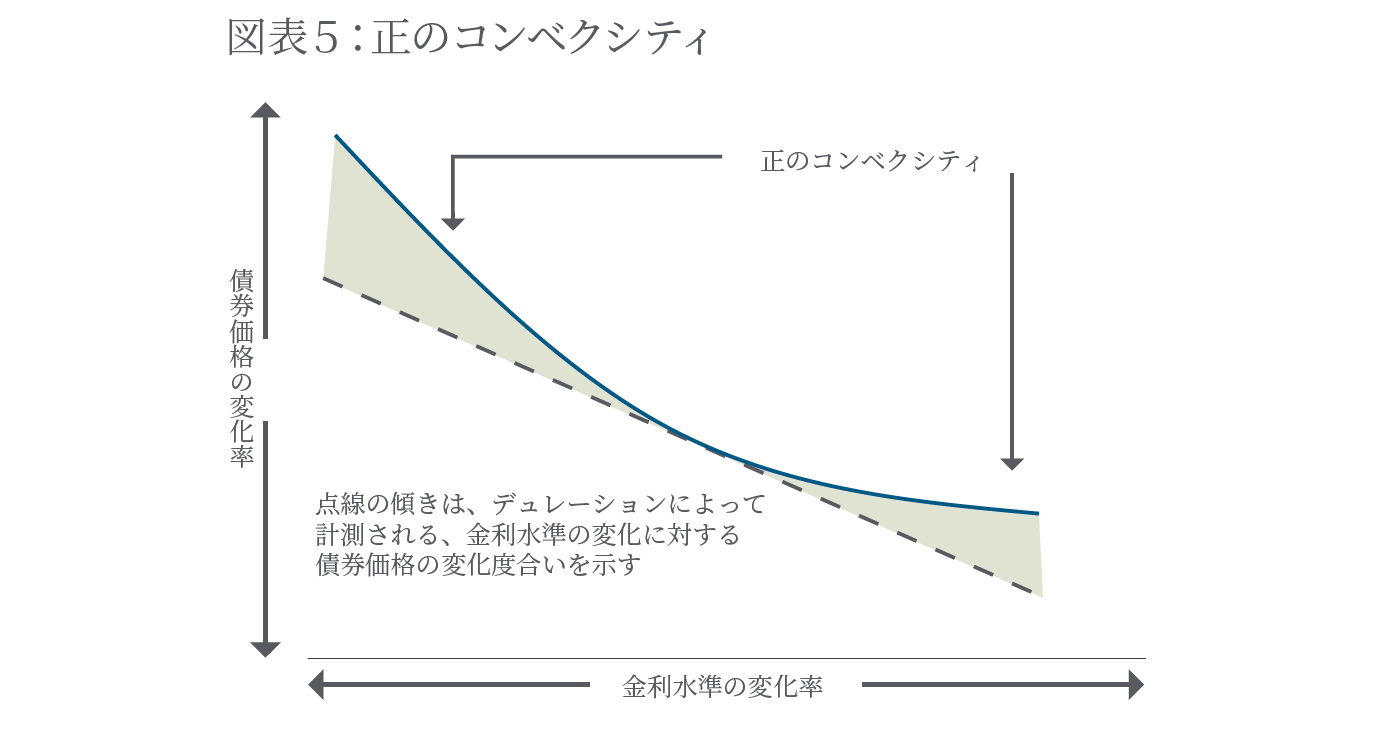
正のコンベクシティ
オプションを内包しない国債等の債券では、金利が低下したときに 債券価格が上昇する割合の方が、同単位の金利が上昇したときに債 券価格が下落する割合よりも大きくなります。下記の図では、青色の 実線が、金利変化による実際の債券価格の変化を示し、点線の傾 きがデュレーションによって計測される、金利変化による債券価格 の変化率を示します。コンベクシティが正である場合、金利低下時 は、債券価格は点線の傾き以上に上昇し、また金利上昇時は点線 の傾きほど債券価格は低下しません。
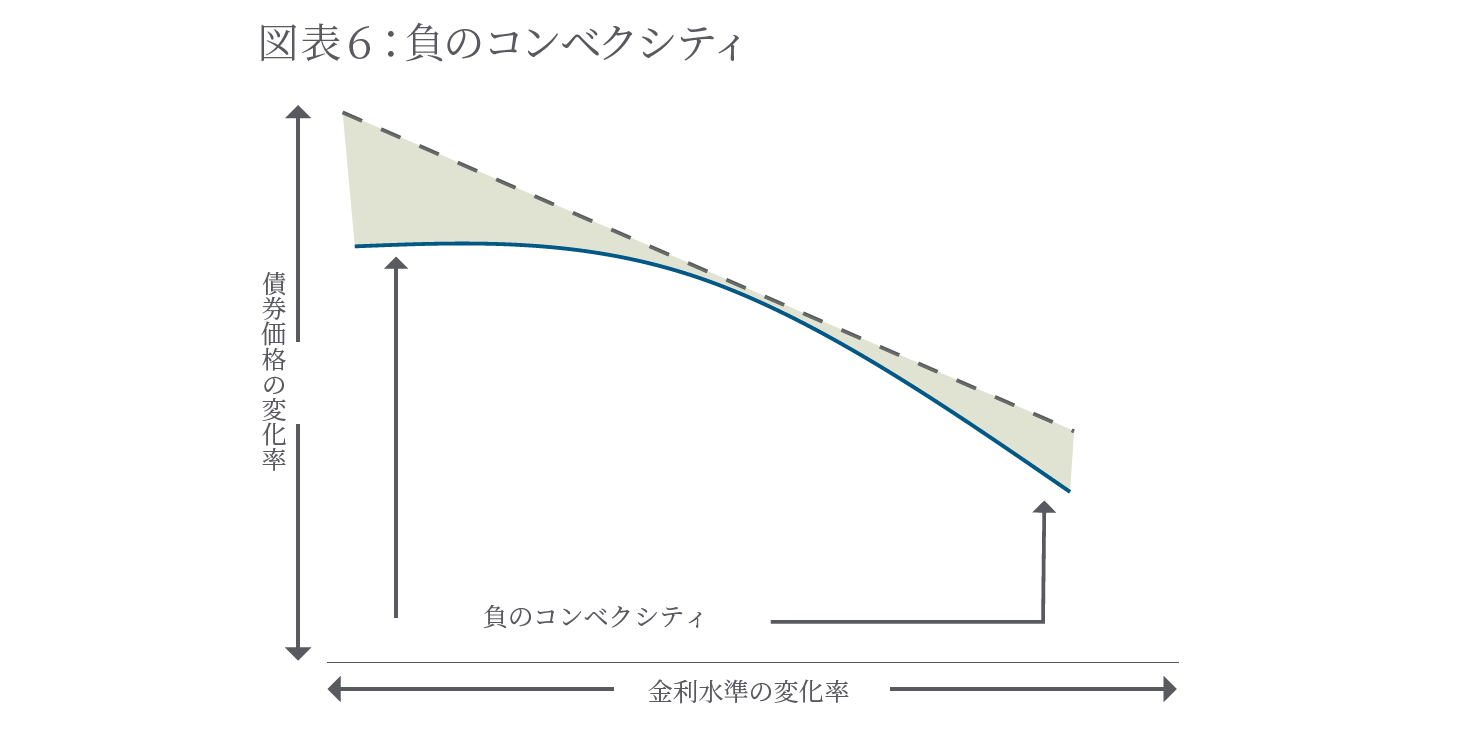
負のコンベクシティ
モーゲージ債のようにオプションの売りを内包している債券は、負 のコンベクシティの性質をもちます。負のコンベクシティは、金利が 低下したときに債券価格が上昇する割合のほうが、同単位の金利が 上昇したときに債券価格が下落する割合よりも小さくなります。下記 の図では、金利低下時は、デュレーションによって計測される債券 価格の変化率(点線の傾き)ほど債券価格は上昇せず、また金利上 昇時はこの傾き以上に価格が低下します。
デュレーションによる計測では、金利の上昇および低下に対して常に 同率(点線)の債券価格変化となるため、金利水準の変化が大きく なるほど、コンベクシティの性質を捕捉することが困難になります。
コンベクシティの計測は、オプションを内包しない債券であれば、 満期までの債券保有によるキャッシュフローが確定しているため、 さほど複雑なものとはなりませんが、オプションを内包している債 券については、将来のオプション行使によるキャッシュフローの変 化を予測せねばならず、高度な計量モデルの構築が必要となりま す。ただし、どんなにモデルの精度を向上させたとしても、モデルに より常に完全な予測ができるものではありません。